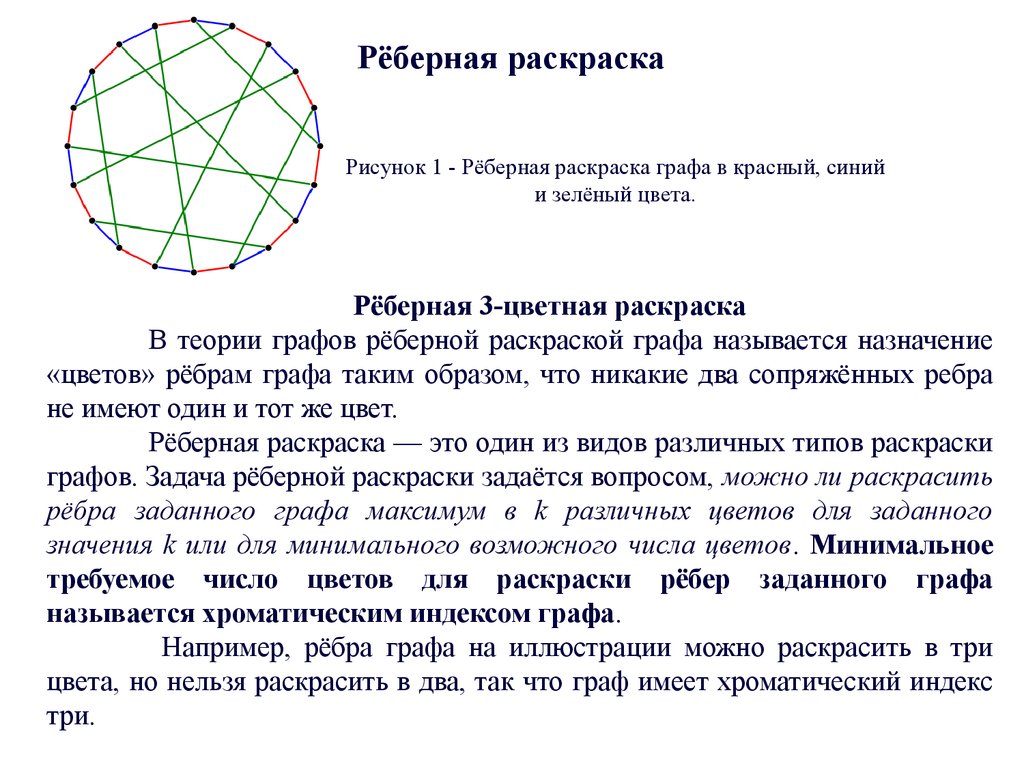
Реберная раскраска
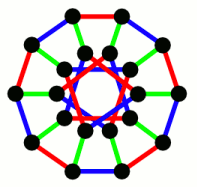
Графы. Раскраска графов. (Тема 3)
Граф называется реберно - раскрашиваемым , если его ребра можно раскрасить красками таким образом, что никакие два смежных ребра не окажутся одного цвета. Если граф реберно -раскрашиваем, но не является реберно -раскрашиваемым, то называется хроматическим классом или хроматическим индексом , или реберно-хроматическим числом графа. При этом используется запись. На рисунке изображен граф , для которого. Ясно, что если наибольшая из степеней вершин графа равна , то.


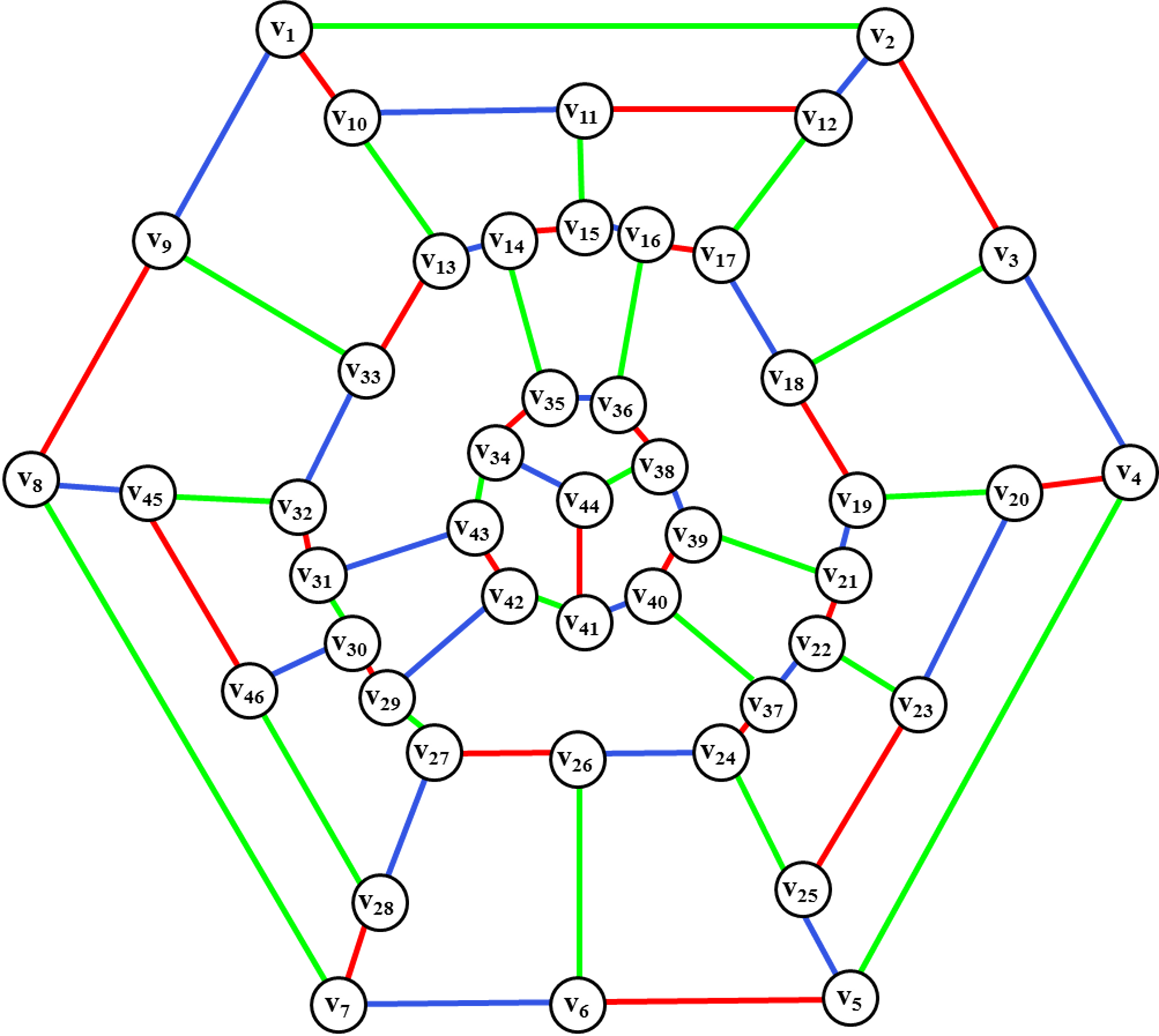







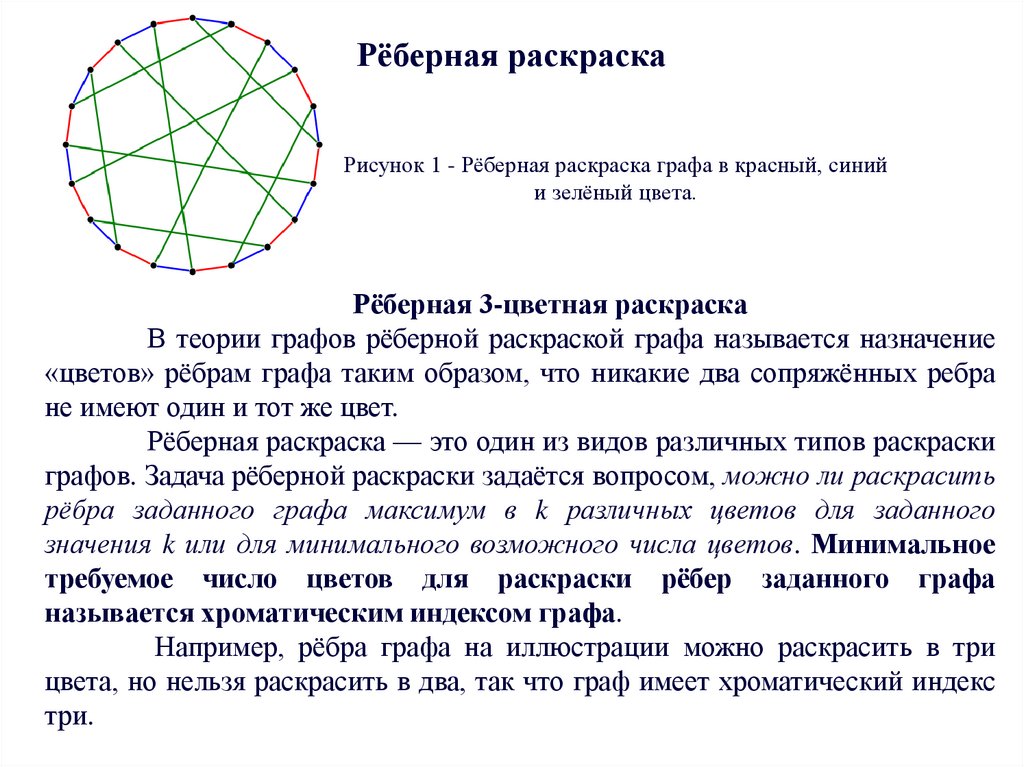


Рёберная раскраска — назначение «цветов» рёбрам графа таким образом, что никакие два смежных ребра не имеют один и тот же цвет. Рёберная раскраска — это один из видов различных типов раскраски графов. Задача рёберной раскраски задаётся вопросом, можно ли раскрасить рёбра заданного графа максимум в различных цветов для заданного значения или для минимального возможного числа цветов. Минимальное требуемое число цветов для раскраски рёбер заданного графа называется хроматическим индексом графа. Например, рёбра графа на иллюстрации можно раскрасить в три цвета, но нельзя раскрасить в два, так что граф имеет хроматический индекс 3.
- Хроматическое число графа G — минимальное число цветов, в которые можно раскрасить вершины графа G так, чтобы концы любого ребра имели разные цвета.
- Рёберная раскраска — назначение «цветов» рёбрам графа таким образом, что никакие два смежных ребра не имеют один и тот же цвет. Рёберная раскраска — это один из видов различных типов раскраски графов.
- Раскраска графа — теоретико-графовая конструкция, частный случай разметки графа.



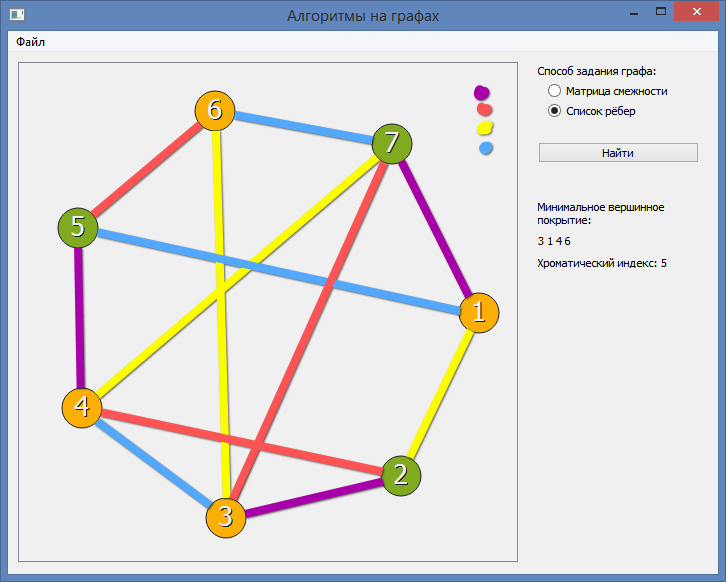






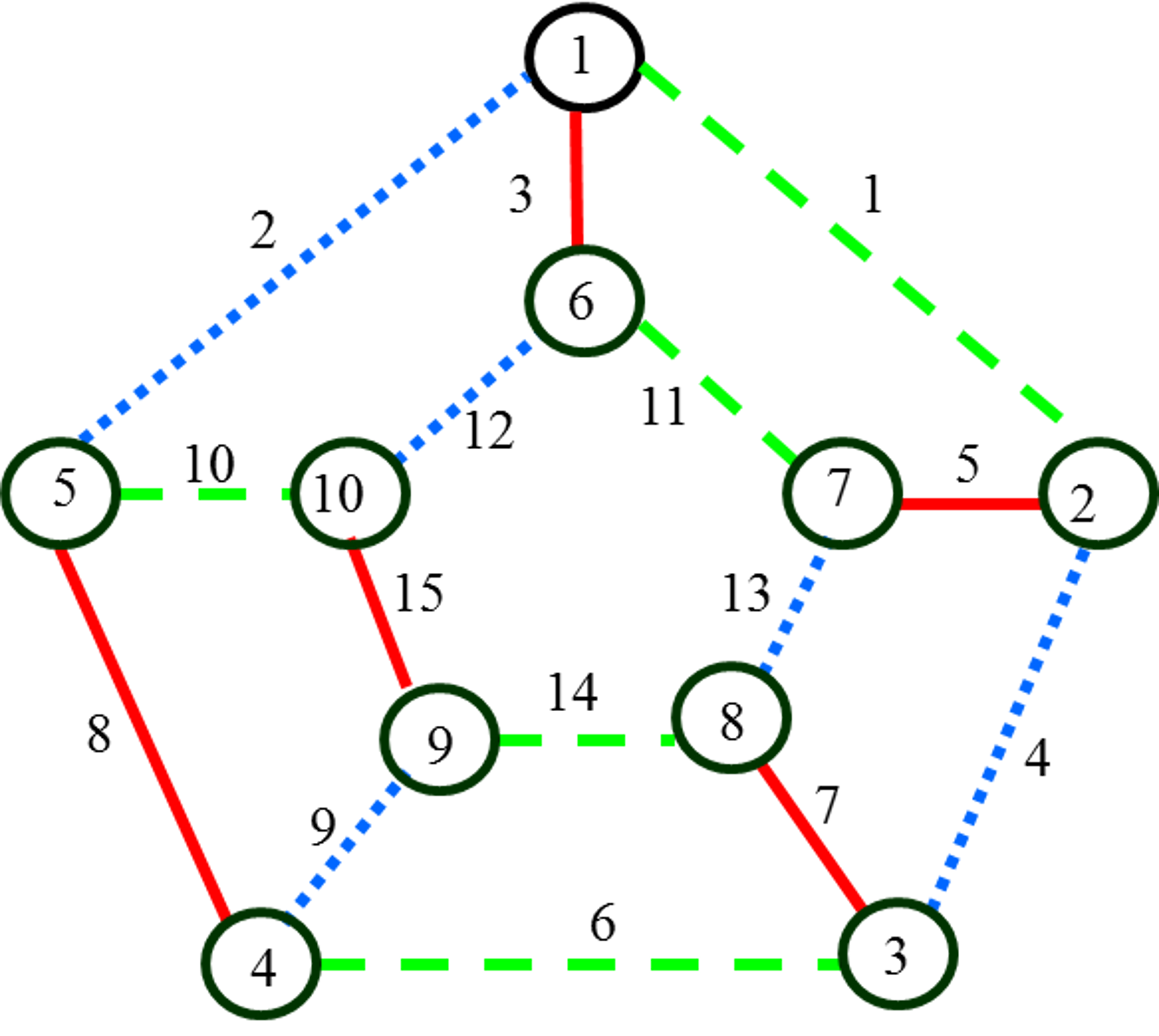
Иногда требуется в разные цвета окрасить ребра графа так, чтобы смежные ребра имели разные цвета. Решить задачу о числе необходимых красок для такой раскраски ребер можно с помощью рассмотренных алгоритмов раскраски вершин графа. Для этого надо превратить ребра в вершины и соединить полученные вершины так, что две вершины соединяются ребром, если в исходном графе ребра были смежны.