Раскраска графов теоремы о раскраске графов

Основы теории графов 09: раскраски планарных графов, совершенные графы
Рассматриваем раскраски планарных графов и другие темы, связанные с раскрасками. Доказываем теорему Томассена о том, что списочное хроматическое число любого планарного графа не превышает пяти. Доказываем теорему Эрдёша о том, что существуют графы с большим хроматическим числом и одновременно большим обхватом. Рассматриваем совершенные графы и доказываем слабую гипотезу Бержа.


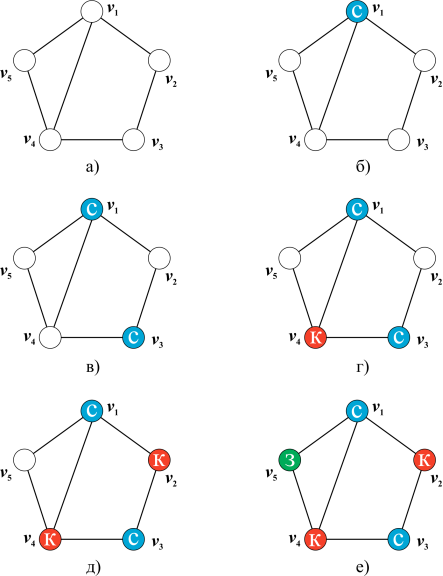





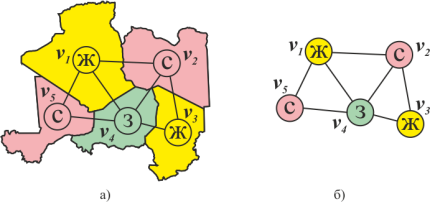


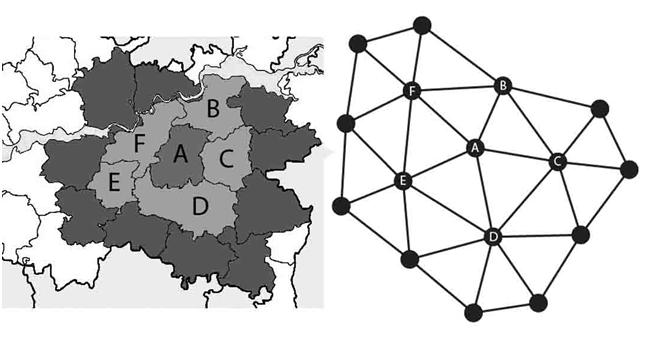
Теорема о четырех цветах — это математический вопрос, который возник еще в 19 веке. Он заключается в том, можно ли раскрасить любую карту, используя только четыре цвета, таким образом, чтобы ни одна из двух соседних областей не имела одинакового цвета. В этом материале мы расскажем, у кого впервые возник этот вопрос, причем тут теория графов, кто и как пытался доказать эту теорему и что из этого вышло. Первоначально вопросом четырех цветов заинтересовался студент Фредерик Гатри, который изучал карту графств Англии. Гатри заметил, что для того, чтобы два соседних графства были разных цветов, необходимо всего четыре цвета. Это наблюдение заставило его задаться вопросом, возможно ли применить этот принцип к любой карте, будь то весь мир, страна или группа островов.


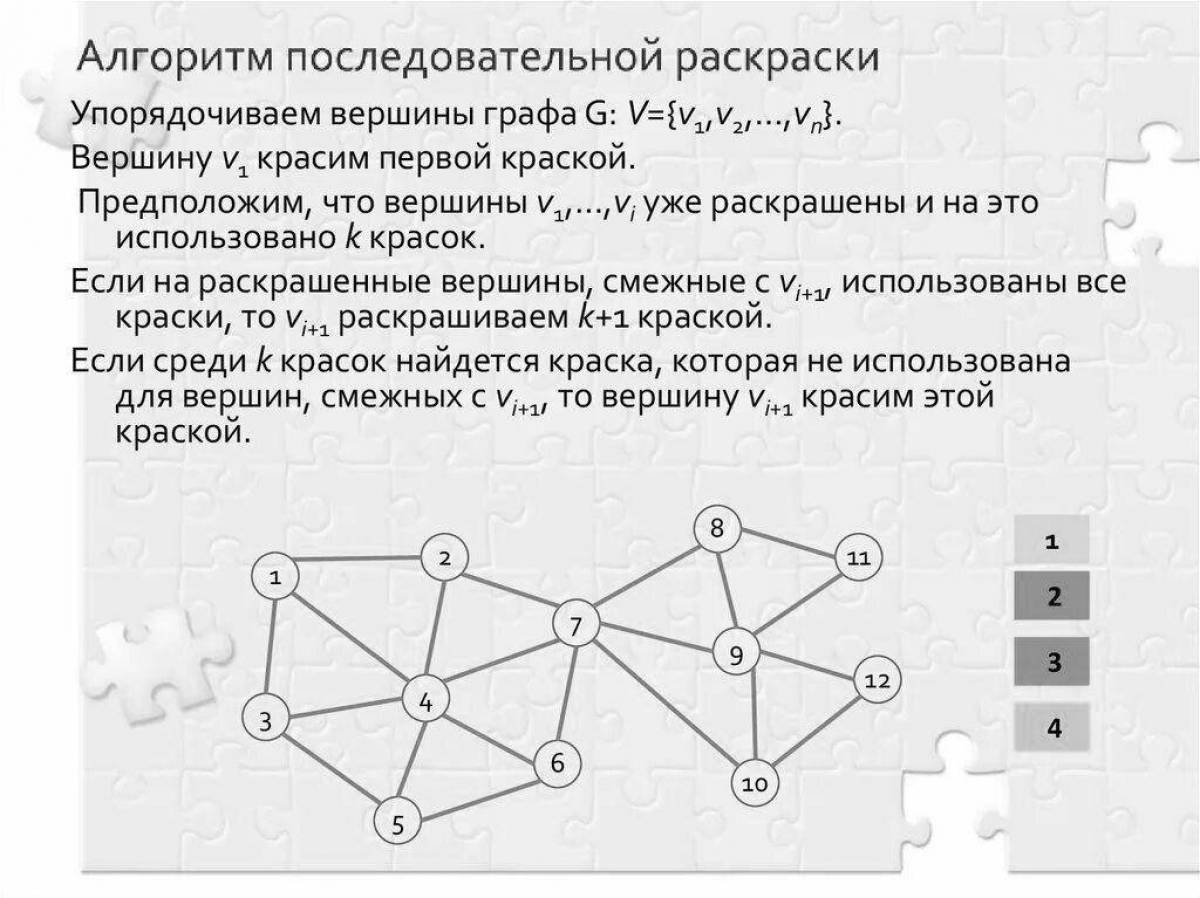






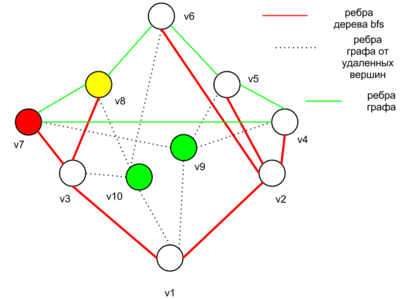

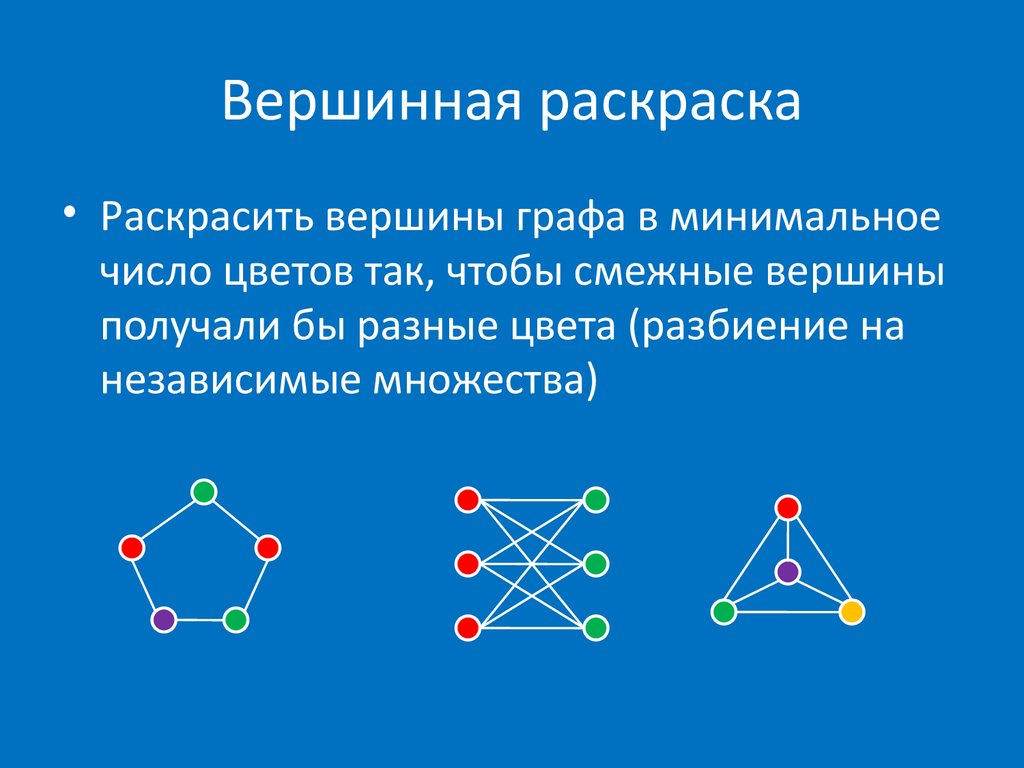
Корректной раскраской графа в два цвета называется такая раскраска, что никакое ребро не соединяет две вершины одного цвета. Графы, которые можно так раскрасить, называют двудольными. Заметим, что если такая раскраска существует, и если зафиксировать цвет одной вершины, то все цвета всех достижимых из неё вершин определяются однозначно: пусть цвет этой вершины белый, тогда все её соседи будут иметь черный цвет, все вершины на расстоянии 2 будут иметь снова белый цвет, все вершины на расстоянии 3 снова черный, и так далее. Проверять граф на двудольность и выводить раскраску можно обходом в глубину. На этот раз наш dfs будет принимать параметром цвет, в который нужно покрасить вершину, и он будет рекурсивно запускаться от всех соседей, крася их в противоположный цвет. По окончании работы алгоритма мы либо обнаружим, что граф не двудолен мы когда-то посмотрели на две соседние вершины, которым нужно присвоить один и тот же цвет , либо найдём разбиение вершин графа на две доли.

.png)