Как сделать логарифмы с одинаковым основанием

Вы знаете, какая тема в математике объединяет рога горных козлов, многие галактики и возможность получить 4 первичных балла на ЕГЭ по профильной математике? Это логарифм и его свойства! Но обо всем по порядку.

Действия с логарифмами. Набиваем руку!

Мы можем встретить в вычислительных задачах степени различных чисел в разных сочетаниях, например, при вычислении выражения надо возводить в степень разные числа, умножать и делить степени. Зачем так много степеней? Нельзя ли обойтись степенями какого-то одного основания? Конечно, можно. Первое правило Можно выбрать одно удобное основание, например а , и привести любую степень к основанию а , то есть представить любую степень в виде при некотором k.

Регистрация Вход. Ответы Mail. Вопросы - лидеры. Пожалуйста, помогите решить 1 ставка. Пожалуйста , помогите решить.

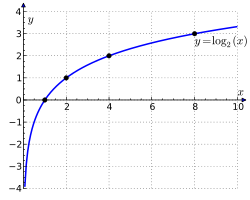
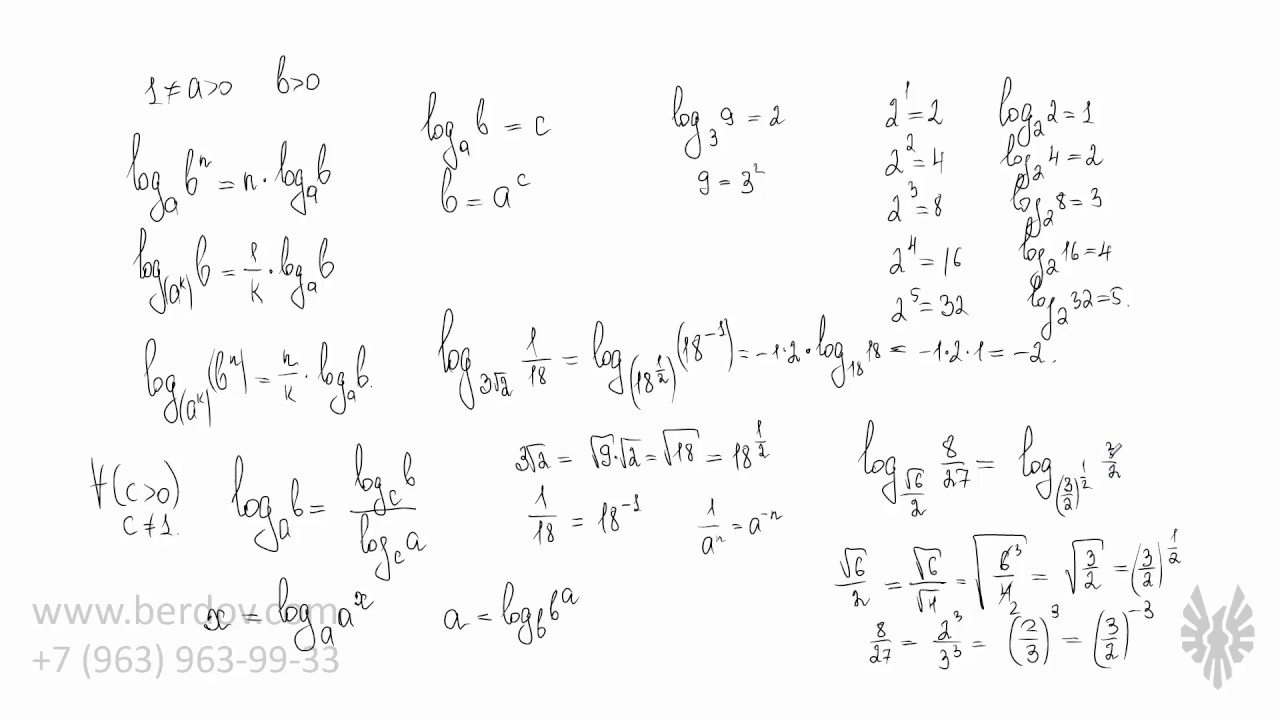
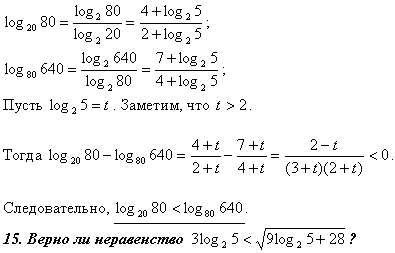
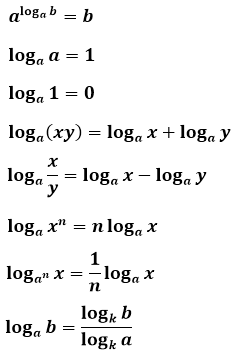
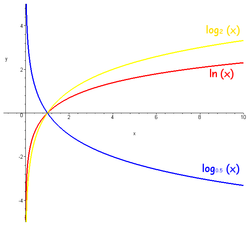
Если , , — положительные числа, причем a и c отличны от 1, то имеет место равенство: — формула перехода к новому основанию. Преобразуем данное равенство, домножив левую и правую часть на знаменатель правой части:. Далее возведем в степень левой и правой части:. Мы получили равенство, которое верно по основному логарифмическому тождеству.

Похожие статьи

• В первый день в мастерской сшили 19 одинаковых рюкзаков во второй 23
• Кровать с основанием чертежи
• Чепчик новорожденному 5 урок Одежда Юбка полусолнце
• Лодки из фанеры видео чертежи - Стулья из фанеры своими руками: фото чертежи стула, видео